Modular lambda function

In mathematics, the elliptic modular lambda function 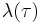$\lambda(\tau)$ is a highly symmetric holomorphic function on the complex upper half-plane. It is invariant under the fractional linear action of the congruence group 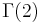$\Gamma(2)$ , and generates the function field of the corresponding quotient, i.e., it is a Hauptmodul for the modular curve 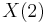$X(2)$ . 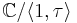Over any point $\tau$ , its value can be described as a cross ratio of the branch points of a ramified double cover of the projective line by the elliptic curve $\mathbb{C}/\langle 1, \tau \rangle$ , where the map is defined as the quotient by the $[-1]$ involution.

The q-expansion is given by:

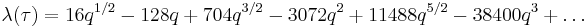$\lambda(\tau) = 16q^{1/2} - 128q %2B 704 q^{3/2} - 3072q^2 %2B 11488q^{5/2} - 38400q^3 %2B \dots$ .

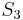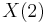By symmetrizing the lambda function under the canonical action of the symmetric group $S_3$ on $X(2)$ , and then normalizing suitably, one obtains a function on the upper half-plane that is invariant under the full modular group 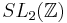$SL_2(\mathbb{Z})$ , and it is in fact Klein's modular j-invariant.

Other appearances

It is the square of the Jacobi modulus, i.e., 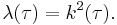$\lambda(\tau) = k^2 (\tau). \,$ .

The function 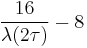$\frac{16}{\lambda(2\tau)} - 8$ is the normalized Hauptmodul for the group 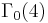$\Gamma_0(4)$ , and its q-expansion 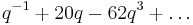$q^{-1} %2B 20q - 62q^3 %2B \dots$ is the graded character of any element in conjugacy class 4C of the monster group acting on the monster vertex algebra.

References

Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, ISBN 978-0-486-61272-0
Conway, John Horton; Norton, Simon (1979), "Monstrous moonshine", Bulletin of the London Mathematical Society 11 (3): 308–339, doi:10.1112/blms/11.3.308, MR 0554399 .

Modular lambda function

Other appearances

References

External links